Problem Description

We have 30 projects from our clients. Each project has a deadline, the number of days it will take us to complete, and a required number of employees to work on it. Here is the project data. 

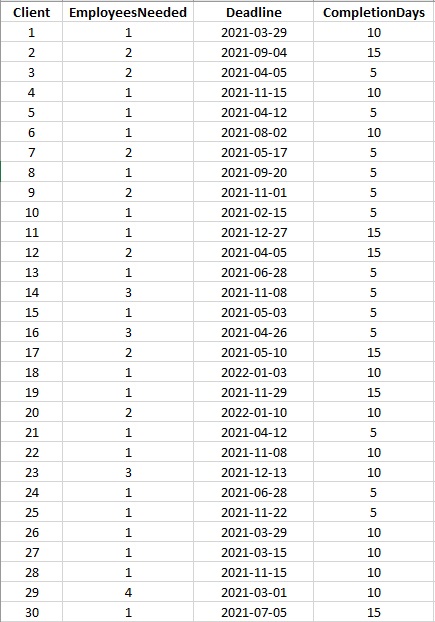
As long as a project is completed on or before the deadline, its starting date is flexible. For example, a project takes two days to complete and has Friday as the deadline. The last possible starting date is Wednesday, but we can start on Monday or Tuesday and complete the project earlier than the deadline. This is the flexible date part of the scheduling problem.

We have 6 employees and each of them has a score for their overall skill. The higher the score, the better the skill set and thus, more likely to improve client satisfaction. If an employee is assigned to a project, then he becomes unavailable for other projects until the assigned one is complete. Here is the employee data. 

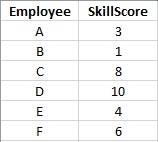
The goal is to schedule our employees in a way that maximizes total client satisfaction.

Algorithm

We can express the above description in a mathematical form. In other words, we translate it into an optimization problem with parameters, variables, objective function, and constraints.

Key parameters

[Client, Date]: the combo of (client, one of its possible starting dates)

Skill[Employee]: for each employee, there is a skill score used to approximate client satisfaction.

Variable (chosen by the optimizer)

Assignment[Employee, Client, Date]: 1 if Employee is assigned to Client starting on Date, 0 otherwise.

Objective function (maximized by the optimizer)

Sum: Skill[Employee] * Assignment[Employee, Client, Date] over all employees, clients, and starting dates

Constraint 1 - No overlapping schedule for each employee

Conflict[Client i, Date i, Client j, Date j]: 1 if there is a schedule conflict (or i = j), 0 otherwise.

Here is an example showing there is a conflict between [Client 1, Date 1] and [Client 2, Date 2].

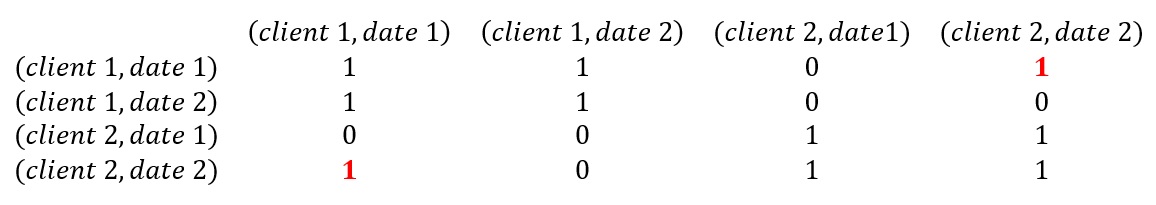
The constraint checks the sum of the following 2 components to make sure it equals to 0. ‍

Case 1: the same (Client, Date) pairs. In other words, [Client 1, Date 1] and [Client 1, Date 1]. 

Component 1: Assignment[Employee A, Client 1, Date 1] * Assignment[Employee A, Client 1, Date 1] * (Conflict[Client 1, Date 1, Client 1, Date 1] - 1) = 0.‍

The first two items should have the same value (either both 0 or both 1). The last item (in italic) should always be 0 because the conflict indicator for the same (client, date) combo is 1 by definition and 1 - 1 = 0. 

Case 2: different (Client, Date) pairs.

Component 2: Assignment[Employee A, Client 1, Date 1] * Assignment[Employee A, Client 2, Date 1] * Conflict[Client 1, Date 1, Client 2, Date 1] = 0.‍

The non-bold, italic part can also be (Client 1, Date 2) or (Client 2, Date 2). 

Subcase 2.1: for combos with no conflict, its conflict indicator is 0, so Component 2 = 0.

Subcase 2.2: for combos with conflict, its conflict indicator is 1. But at least one of the assignments should be 0, otherwise it means that a conflict exists. 

For example, if there is a conflict in assignments as shown in Fig 3, Assignment[Employee A, Client 1, Date 1] * Assignment[Employee A, Client 2, Date 2] * Conflict[Client 1, Date 1, Client 2, Date 2] = 1 * 1 * 1 = 1.

If there is no conflict in assignments, then either Assignment[Employee A, Client 1, Date 1] = 0, or Assignment[Employee A, Client 2, Date 2] = 0, or both are 0. As a result, Assignment[Employee A, Client 1, Date 1] * Assignment[Employee A, Client 2, Date 2] * Conflict[Client 1, Date 1, Client 2, Date 2] = 0 * 1 = 0.

Constraint 2 - All employees start on the same date for each client

This is a non-linear, quadratic constraint. 

Here is an example of the assignment vector for Client 1 by its possible starting dates.

If Date 1 is assigned to Client 1, then all the entries in Vector II should be 0; vice versa. This means for each client, sum of all entries in Vector I * sum of all entries in Vector II = 0.

We can extend the logic to more than 2 possible dates. Say, we have N possible dates. Then check whether the sum of the following N totals is equal to 0:

total n = sum of all entries in Vector I with date n *  sum of all entries in Vector II with the rest of the dates (aka dates that aren't equal to n) where n = 1, 2, …, N.

‍Constraint 3 - Total employees assigned to each client equals to the number of employees needed for the client

For Client i, sum of Assignment[Employee, Client i, Date] over all employees and starting dates should equal to the employee load of Client i.